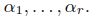Joint discrete approximation of analytic functions by Hurwitz zeta-functions
Abstract
Let H(D) be the space of analytic functions on the strip . In this paper, it is proved that there exists a closed non-empty set
such that every collection of the functions
is approximated by discrete shifts
, of Hurwitz zeta-functions with arbitrary parameters
Keyword : Hurwitz zeta-function, space of analytic functions, weak convergence, universality
How to Cite
Balčiūnas, A., Garbaliauskienė, V., Lukšienė, V., Macaitienė, R., & Rimkevičienė, A. (2022). Joint discrete approximation of analytic functions by Hurwitz zeta-functions. Mathematical Modelling and Analysis, 27(1), 88–100. https://doi.org/10.3846/mma.2022.15068

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
B. Bagchi. The Statistical Behaviuor and Universality Properties of the Riemann Zeta-Function and Other Allied Dirichlet Series. PhD Thesis, Indian Statistical Institute, Calcutta, 1981.
A. Balčiūnas, A. Dubickas and A. Laurinčikas. On the Hurwitz zeta-function with algebraic irrational parameter. Math. Notes, 105(1-2):173–179, 2019. https://doi.org/10.1134/S0001434619010218
A. Balčiūnas, V. Garbaliauskienė, J. Karaliūnaitė, R. Macaitienė, J. Petuškinaitė and A. Rimkevičienė. Joint discrete approximation of a pair of analytic functions by periodic zeta-functions. Math. Modell. Analysis, 25(1):71–87, 2020. https://doi.org/10.3846/mma.2020.10450
P. Billingsley. Convergence of Probability Measures. Willey, New York, 1968.
E. Buivydas and A. Laurinčikas. A discrete version of the Mishou theorem. RamanujanJ., 38(2):331–347, 2015. https://doi.org/10.1007/s11139-014-9631-2
E. Buivydas and A. Laurinčikas. A generalized joint discrete universality theorem for the Riemann and Hurwitz zeta-functions. Lith. Math. J., 55(2):193–206, 2015. https://doi.org/10.1007/s10986-015-9273-0
E. Buivydas, A. Laurinčikas, R. Macaitienė and J. Rašytė. Discrete universality theorems for the Hurwitz zeta-function. J. Approx. Th., 183:1–13, 2014. https://doi.org/10.1016/j.jat.2014.03.006
V. Franckeviče, A. Laurinčikas and D. Šiaučiūnas. On joint value distribution of Hurwitz zeta-functions. Chebyshevskii Sb., 19(3):219–230, 2018.
V. Franckevič, A. Laurinčikas and D. Šiaučiūnas. On approximation of analytic functions by periodic Hurwitz zeta-functions. Math. Modell. Analysis, 24(1):20– 33, 2019. https://doi.org/10.3846/mma.2019.002
S.M. Gonek. Analytic Properties of Zeta and L-Functions. PhD Thesis, University of Michigan, 1979.
A. Javtokas and A. Laurinčikas. Universality of the periodic Hurwitz zeta-function. Integral Transforms Spec. Funct., 17(10):711–722, 2006. https://doi.org/10.1080/10652460600856484
R. Kačinskaitė and A. Laurinčikas. The joint distribution of periodic zeta-functions. Studia Sci. Math. Hungar., 48(2):257–279, 2011. https://doi.org/10.1556/sscmath.48.2011.2.1162
A. Laurinčikas. The joint universality of Hurwitz zeta-functions. Siauliai Math. Semin., 3 (11):169–187, 2008.
A. Laurinčikas. Joint universality of zeta-functions with periodic coefficients. Izv. Math., 74(3):515–539, 2010. https://doi.org/10.1070/IM2010v074n03ABEH002497
A. Laurinčikas. A discrete universality theorem for the Hurwitz zeta-function. J. Number Th., 143:232–247, 2014. https://doi.org/10.1016/j.jnt.2014.04.013
A. Laurinčikas. Distribution modulo 1 and universality of the Hurwitz zeta-function. J. Number Th., 167:294–303, 2016. https://doi.org/10.1016/j.jnt.2016.03.013
A. Laurinčikas. Universality theorems for zeta-functions with periodic coefficients. Siber. Math. J., 57(2):330–339, 2016. https://doi.org/10.1134/S0037446616020154
A. Laurinčikas. A discrete version of the Mishou theorem. II. Proc. Steklov Inst. Math., 296(1):172–182, 2017. https://doi.org/10.1134/S008154381701014X
A. Laurinčikas. On discrete universality of the Hurwitz zeta-function. Results Math., 72(1-2):907–917, 2017. https://doi.org/10.1007/s00025-017-0702-8
A. Laurinčikas. Joint value distribution theorems for the Riemann and Hurwitz zeta-functions. Moscow Math. J., 18(2):349–366, 2018. https://doi.org/10.17323/1609-4514-2018-18-2-349-366
A. Laurinčikas. “Almost” universality of the Lerch zeta-function. Math. Commun., 24(1):107–118, 2019.
A. Laurinčikas. Joint discrete universality for periodic zeta-functions. Quaest. Math., 42(5):687–699, 2019. https://doi.org/10.2989/16073606.2018.1481891
A. Laurinčikas. Non-trivial zeros of the Riemann zeta-function and joint universality theorems. J. Math. Anal. Appl., 475(1):385–402, 2019. https://doi.org/10.1016/j.jmaa.2019.02.047
A. Laurinčikas. On the Mishou theorem with algebraic parameter. Siber. Math. J., 60(6):1075–1082, 2019. https://doi.org/10.1134/S0037446619060144
A. Laurinčikas. Joint discrete universality for periodic zeta-functions. II. Quaest. Math., 43(12):1765–1779, 2020. https://doi.org/10.2989/16073606.2019.1654554
A. Laurinčikas. Zeros of the Riemann zeta-function in the discrete universality of the Hurwitz zeta-function. Studia Sci. Math. Hungar., 57(2):147–164, 2020. https://doi.org/10.1556/012.2020.57.2.1460
A. Laurinčikas. On the Hurwitz zeta-function with algebraic irrational parameter. Proc. Steklov Inst. Math., http://mi.mathnet.ru/tm4165
A. Laurinčikas and R. Garunkštis. The Lerch Zeta-Function. Kluwer Academic Publishers, Dordrecht, Boston, London, 2002.
A. Laurinčikas and R. Macaitienė. The discrete universality of the periodic Hurwitz zeta function. Integral Transforms Spec. Funct., 20(9-10):673–686, 2009. https://doi.org/10.1080/10652460902742788
A. Laurinčikas and R. Macaitienė. Joint approximation of analytic functions by shifts of the Riemann and periodic Hurwitz zeta-functions. Appl. Anal. Discrete Math., 12(2):508–527, 2018. https://doi.org/10.2298/AADM170713016L
A. Laurinčikas, R. Macaitienė, D. Mochov and D. Šiaučiūnas. Universality of the periodic Hurwitz zeta-function with rational parameter. Sib. Math. J., 59(5):894–900, 2018. https://doi.org/10.1134/S0037446618050130
R. Macaitienė and D. Šiaučiūnas. Joint universality of Hurwitz zeta-functions and nontrivial zeros of the Riemann zeta-function. Lith. Math. J., 59(1):81–95, 2019. https://doi.org/10.1007/s10986-019-09423-2
H. Mishou. The joint value distribution of the Rieman zeta-function and Hurwitz zeta-functions. Lith. Math. J., 47(1):32–47, 2007. https://doi.org/10.1007/s10986-007-0003-0
H.L. Montgomery. Topics in Multiplicative Number Theory. Lecture Notes Math. Vol. 227, Springer-Verlag, Berlin, 1971. https://doi.org/10.1007/BFb0060851
J. Sander and J. Steuding. Joint universality for sums and products of Dirichlet L-functions. Analysis (Munich), 26(3):295–312, 2006. https://doi.org/10.1524/anly.2006.26.99.295
S.M. Voronin. Analytic Properties of Generating Function of Arithmetic Objects. Diss. doktor fiz.-matem. nauk, Steklov Math. Inst., Moscow, 1977 (in Russian).
A. Balčiūnas, A. Dubickas and A. Laurinčikas. On the Hurwitz zeta-function with algebraic irrational parameter. Math. Notes, 105(1-2):173–179, 2019. https://doi.org/10.1134/S0001434619010218
A. Balčiūnas, V. Garbaliauskienė, J. Karaliūnaitė, R. Macaitienė, J. Petuškinaitė and A. Rimkevičienė. Joint discrete approximation of a pair of analytic functions by periodic zeta-functions. Math. Modell. Analysis, 25(1):71–87, 2020. https://doi.org/10.3846/mma.2020.10450
P. Billingsley. Convergence of Probability Measures. Willey, New York, 1968.
E. Buivydas and A. Laurinčikas. A discrete version of the Mishou theorem. RamanujanJ., 38(2):331–347, 2015. https://doi.org/10.1007/s11139-014-9631-2
E. Buivydas and A. Laurinčikas. A generalized joint discrete universality theorem for the Riemann and Hurwitz zeta-functions. Lith. Math. J., 55(2):193–206, 2015. https://doi.org/10.1007/s10986-015-9273-0
E. Buivydas, A. Laurinčikas, R. Macaitienė and J. Rašytė. Discrete universality theorems for the Hurwitz zeta-function. J. Approx. Th., 183:1–13, 2014. https://doi.org/10.1016/j.jat.2014.03.006
V. Franckeviče, A. Laurinčikas and D. Šiaučiūnas. On joint value distribution of Hurwitz zeta-functions. Chebyshevskii Sb., 19(3):219–230, 2018.
V. Franckevič, A. Laurinčikas and D. Šiaučiūnas. On approximation of analytic functions by periodic Hurwitz zeta-functions. Math. Modell. Analysis, 24(1):20– 33, 2019. https://doi.org/10.3846/mma.2019.002
S.M. Gonek. Analytic Properties of Zeta and L-Functions. PhD Thesis, University of Michigan, 1979.
A. Javtokas and A. Laurinčikas. Universality of the periodic Hurwitz zeta-function. Integral Transforms Spec. Funct., 17(10):711–722, 2006. https://doi.org/10.1080/10652460600856484
R. Kačinskaitė and A. Laurinčikas. The joint distribution of periodic zeta-functions. Studia Sci. Math. Hungar., 48(2):257–279, 2011. https://doi.org/10.1556/sscmath.48.2011.2.1162
A. Laurinčikas. The joint universality of Hurwitz zeta-functions. Siauliai Math. Semin., 3 (11):169–187, 2008.
A. Laurinčikas. Joint universality of zeta-functions with periodic coefficients. Izv. Math., 74(3):515–539, 2010. https://doi.org/10.1070/IM2010v074n03ABEH002497
A. Laurinčikas. A discrete universality theorem for the Hurwitz zeta-function. J. Number Th., 143:232–247, 2014. https://doi.org/10.1016/j.jnt.2014.04.013
A. Laurinčikas. Distribution modulo 1 and universality of the Hurwitz zeta-function. J. Number Th., 167:294–303, 2016. https://doi.org/10.1016/j.jnt.2016.03.013
A. Laurinčikas. Universality theorems for zeta-functions with periodic coefficients. Siber. Math. J., 57(2):330–339, 2016. https://doi.org/10.1134/S0037446616020154
A. Laurinčikas. A discrete version of the Mishou theorem. II. Proc. Steklov Inst. Math., 296(1):172–182, 2017. https://doi.org/10.1134/S008154381701014X
A. Laurinčikas. On discrete universality of the Hurwitz zeta-function. Results Math., 72(1-2):907–917, 2017. https://doi.org/10.1007/s00025-017-0702-8
A. Laurinčikas. Joint value distribution theorems for the Riemann and Hurwitz zeta-functions. Moscow Math. J., 18(2):349–366, 2018. https://doi.org/10.17323/1609-4514-2018-18-2-349-366
A. Laurinčikas. “Almost” universality of the Lerch zeta-function. Math. Commun., 24(1):107–118, 2019.
A. Laurinčikas. Joint discrete universality for periodic zeta-functions. Quaest. Math., 42(5):687–699, 2019. https://doi.org/10.2989/16073606.2018.1481891
A. Laurinčikas. Non-trivial zeros of the Riemann zeta-function and joint universality theorems. J. Math. Anal. Appl., 475(1):385–402, 2019. https://doi.org/10.1016/j.jmaa.2019.02.047
A. Laurinčikas. On the Mishou theorem with algebraic parameter. Siber. Math. J., 60(6):1075–1082, 2019. https://doi.org/10.1134/S0037446619060144
A. Laurinčikas. Joint discrete universality for periodic zeta-functions. II. Quaest. Math., 43(12):1765–1779, 2020. https://doi.org/10.2989/16073606.2019.1654554
A. Laurinčikas. Zeros of the Riemann zeta-function in the discrete universality of the Hurwitz zeta-function. Studia Sci. Math. Hungar., 57(2):147–164, 2020. https://doi.org/10.1556/012.2020.57.2.1460
A. Laurinčikas. On the Hurwitz zeta-function with algebraic irrational parameter. Proc. Steklov Inst. Math., http://mi.mathnet.ru/tm4165
A. Laurinčikas and R. Garunkštis. The Lerch Zeta-Function. Kluwer Academic Publishers, Dordrecht, Boston, London, 2002.
A. Laurinčikas and R. Macaitienė. The discrete universality of the periodic Hurwitz zeta function. Integral Transforms Spec. Funct., 20(9-10):673–686, 2009. https://doi.org/10.1080/10652460902742788
A. Laurinčikas and R. Macaitienė. Joint approximation of analytic functions by shifts of the Riemann and periodic Hurwitz zeta-functions. Appl. Anal. Discrete Math., 12(2):508–527, 2018. https://doi.org/10.2298/AADM170713016L
A. Laurinčikas, R. Macaitienė, D. Mochov and D. Šiaučiūnas. Universality of the periodic Hurwitz zeta-function with rational parameter. Sib. Math. J., 59(5):894–900, 2018. https://doi.org/10.1134/S0037446618050130
R. Macaitienė and D. Šiaučiūnas. Joint universality of Hurwitz zeta-functions and nontrivial zeros of the Riemann zeta-function. Lith. Math. J., 59(1):81–95, 2019. https://doi.org/10.1007/s10986-019-09423-2
H. Mishou. The joint value distribution of the Rieman zeta-function and Hurwitz zeta-functions. Lith. Math. J., 47(1):32–47, 2007. https://doi.org/10.1007/s10986-007-0003-0
H.L. Montgomery. Topics in Multiplicative Number Theory. Lecture Notes Math. Vol. 227, Springer-Verlag, Berlin, 1971. https://doi.org/10.1007/BFb0060851
J. Sander and J. Steuding. Joint universality for sums and products of Dirichlet L-functions. Analysis (Munich), 26(3):295–312, 2006. https://doi.org/10.1524/anly.2006.26.99.295
S.M. Voronin. Analytic Properties of Generating Function of Arithmetic Objects. Diss. doktor fiz.-matem. nauk, Steklov Math. Inst., Moscow, 1977 (in Russian).