On the regularity criterion on one velocity component for the micropolar fluid equations
Abstract
In this paper, we establish a regularity criterion for micropolar fluid flows in terms of the one component of the velocity in critical Morrey-Campanato space. More precisely, we show that if 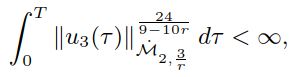
then the weak solution (u,w) is regular.
Keyword : micropolar fluid equations, weak solutions, regularity criterion, Morrey-Campanato spaces
How to Cite
Agarwal, R. P., Alghamdi, A. M., Gala, S., & Ragusa, M. A. (2023). On the regularity criterion on one velocity component for the micropolar fluid equations. Mathematical Modelling and Analysis, 28(2), 271–284. https://doi.org/10.3846/mma.2023.15261

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
C. Cao and E.S. Titi. Regularity criteria for the three-dimensional Navier-Stokes equations. Indiana Univ. Math. J., 57(6):2643–2661, 2008. https://doi.org/10.1512/iumj.2008.57.3719
C. Cao and E.S. Titi. Global regularity criterion for the 3D Navier-Stokes equations involving one entry of the velocity gradient tensor. Arch. Ration. Mech. Anal., 202(3):919–932, 2011. https://doi.org/10.1007/s00205-011-0439-6
D. Chae and H.-J. Choe. Regularity of solutions to the Navier-Stokes equation. Electron. J. Differential Equations, pp. No. 05, 7, 1999.
D. Chae and J. Wolf. On the Serrin-type condition on one velocity component for the Navier-Stokes equations. Arch. Ration. Mech. Anal., 240(3):1323–1347, 2021. https://doi.org/10.1007/s00205-021-01636-5
J.-Y. Chemin and P. Zhang. On the critical one component regularity for 3-D Navier-Stokes systems. Ann. Sci. Éc. Norm. Supér., 49(1):131–167, 2016. https://doi.org/10.24033/asens.2278
J.-Y. Chemin, P. Zhang and Z. Zhang. On the critical one component regularity for 3-D Navier-Stokes system: general case. Arch. Ration. Mech. Anal., 224(3):871–905, 2017. https://doi.org/10.1007/s00205-017-1089-0
B.-Q. Dong and Z.-M. Chen. Regularity criteria of weak solutions to the three-dimensional micropolar flows. J. Math. Phys., 50(10):103525, 13, 2009. https://doi.org/10.1063/1.3245862
B.-Q. Dong, Y. Jia and Z.-M. Chen. Pressure regularity criteria of the threedimensional micropolar fluid flows. Math. Methods Appl. Sci., 34(5):595–606, 2011. https://doi.org/10.1002/mma.1383
B.-Q. Dong and W. Zhang. On the regularity criterion for three-dimensional micropolar fluid flows in Besov spaces. Nonlinear Anal., 73(7):2334–2341, 2010. https://doi.org/10.1016/j.na.2010.06.029
A.C. Eringen. Theory of micropolar fluids. J. Math. Mech., 16:1–18, 1966. https://doi.org/10.1512/iumj.1967.16.16001
H. Fujita and T. Kato. On the Navier-Stokes initial value problem. I. Arch. Rational Mech. Anal., 16:269–315, 1964. https://doi.org/10.1007/BF00276188
S. Gala. On regularity criteria for the three-dimensional micropolar fluid equations in the critical Morrey-Campanato space. Nonlinear Anal. Real World Appl., 12(4):2142–2150, 2011. https://doi.org/10.1016/j.nonrwa.2010.12.028
S. Gala. A remark on the logarithmically improved regularity criterion for the micropolar fluid equations in terms of the pressure. Math. Methods Appl. Sci., 34(16):1945–1953, 2011. https://doi.org/10.1002/mma.1488
G.P. Galdi and S. Rionero. A note on the existence and uniqueness of solutions of the micropolar fluid equations. Internat. J. Engrg. Sci., 15(2):105–108, 1977. https://doi.org/10.1016/0020-7225(77)90025-8
C. He. Regularity for solutions to the Navier-Stokes equations with one velocity component regular. Electron. J. Differential Equations, pp. No. 29, 13, 2002.
L. Iskauriaza, G.A. Ser¨egin and V. Shverak. L3,∞-solutions of Navier-Stokes equations and backward uniqueness. Uspekhi Mat. Nauk, 58(2(350)):3–44, 2003. https://doi.org/10.1070/RM2003v058n02ABEH000609
I. Kukavica and M. Ziane. One component regularity for the Navier-Stokes equations. Nonlinearity, 19(2):453–469, 2006. https://doi.org/10.1088/0951-7715/19/2/012
P.G. Lemari´e-Rieusset. The Navier-Stokes equations in the critical Morrey-Campanato space. Rev. Mat. Iberoam., 23(3):897–930, 2007. https://doi.org/10.4171/RMI/518
S. Machihara and T. Ozawa. Interpolation inequalities in Besov spaces. Proc. Amer. Math. Soc., 131(5):1553–1556, 2003. https://doi.org/10.1090/S0002-9939-02-06715-1
J. Neustupa, A. Novotný and P. Penel. An interior regularity of a weak solution to the Navier-Stokes equations in dependence on one component of velocity. In Topics in mathematical fluid mechanics, volume 10 of Quad. Mat., pp. 163–183. Dept. Math., Seconda Univ. Napoli, Caserta, 2002.
J. Neustupa and P. Penel. Regularity of a suitable weak solution to the NavierStokes equations as a consequence of regularity of one velocity component. In Applied nonlinear analysis, pp. 391–402. Kluwer/Plenum, New York, 1999. https://doi.org/10.1007/0-306-47096-9_26
T. Ohyama. Interior regularity of weak solutions of the timedependent Navier-Stokes equation. Proc. Japan Acad., 36:273–277, 1960. https://doi.org/10.3792/pja/1195524029
E. Ortega-Torres and M. Rojas-Medar. On the regularity for solutions of the micropolar fluid equations. Rend. Semin. Mat. Univ. Padova, 122:27–37, 2009. https://doi.org/10.4171/RSMUP/122-3
P. Penel and M. Pokorný. Some new regularity criteria for the Navier-Stokes equations containing gradient of the velocity. Appl. Math., 49(5):483–493, 2004. https://doi.org/10.1023/B:APOM.0000048124.64244.7e
G. Prodi. Un teorema di unicità per le equazioni di Navier-Stokes. Ann. Mat. Pura Appl., 48:173–182, 1959. https://doi.org/10.1007/BF02410664
J. Serrin. On the interior regularity of weak solutions of the Navier-Stokes equations. Arch. Rational Mech. Anal., 9:187–195, 1962. https://doi.org/10.1007/BF00253344
J. Serrin. The initial value problem for the Navier-Stokes equations. In Nonlinear Problems (Proc. Sympos., Madison, Wis., 1962), pp. 69–98. Univ. Wisconsin Press, Madison, Wis., 1963.
S. Takahashi. On interior regularity criteria for weak solutions of the Navier-Stokes equations. Manuscripta Math., 69(3):237–254, 1990. https://doi.org/10.1007/BF02567922
G. Łukaszewicz. Micropolar fluids. Modeling and Simulation in Science, Engineering and Technology. Theory and applications. Birkhäuser Boston, Inc., Boston, MA, 1999. https://doi.org/10.1007/978-1-4612-0641-5
B. Yuan. On regularity criteria for weak solutions to the micropolar fluid equations in Lorentz space. Proc. Amer. Math. Soc., 138(6):2025–2036, 2010. https://doi.org/10.1090/S0002-9939-10-10232-9
Y. Zhou. A new regularity criterion for the Navier-Stokes equations in terms of the gradient of one velocity component. Methods Appl. Anal., 9(4):563–578, 2002. https://doi.org/10.4310/MAA.2002.v9.n4.a5
Y. Zhou. A new regularity criterion for weak solutions to the NavierStokes equations. J. Math. Pures Appl. (9), 84(11):1496–1514, 2005. https://doi.org/10.1016/j.matpur.2005.07.003
Y. Zhou and M. Pokorný. On the regularity of the solutions of the NavierStokes equations via one velocity component. Nonlinearity, 23(5):1097–1107, 2010. https://doi.org/10.1088/0951-7715/23/5/004
C. Cao and E.S. Titi. Global regularity criterion for the 3D Navier-Stokes equations involving one entry of the velocity gradient tensor. Arch. Ration. Mech. Anal., 202(3):919–932, 2011. https://doi.org/10.1007/s00205-011-0439-6
D. Chae and H.-J. Choe. Regularity of solutions to the Navier-Stokes equation. Electron. J. Differential Equations, pp. No. 05, 7, 1999.
D. Chae and J. Wolf. On the Serrin-type condition on one velocity component for the Navier-Stokes equations. Arch. Ration. Mech. Anal., 240(3):1323–1347, 2021. https://doi.org/10.1007/s00205-021-01636-5
J.-Y. Chemin and P. Zhang. On the critical one component regularity for 3-D Navier-Stokes systems. Ann. Sci. Éc. Norm. Supér., 49(1):131–167, 2016. https://doi.org/10.24033/asens.2278
J.-Y. Chemin, P. Zhang and Z. Zhang. On the critical one component regularity for 3-D Navier-Stokes system: general case. Arch. Ration. Mech. Anal., 224(3):871–905, 2017. https://doi.org/10.1007/s00205-017-1089-0
B.-Q. Dong and Z.-M. Chen. Regularity criteria of weak solutions to the three-dimensional micropolar flows. J. Math. Phys., 50(10):103525, 13, 2009. https://doi.org/10.1063/1.3245862
B.-Q. Dong, Y. Jia and Z.-M. Chen. Pressure regularity criteria of the threedimensional micropolar fluid flows. Math. Methods Appl. Sci., 34(5):595–606, 2011. https://doi.org/10.1002/mma.1383
B.-Q. Dong and W. Zhang. On the regularity criterion for three-dimensional micropolar fluid flows in Besov spaces. Nonlinear Anal., 73(7):2334–2341, 2010. https://doi.org/10.1016/j.na.2010.06.029
A.C. Eringen. Theory of micropolar fluids. J. Math. Mech., 16:1–18, 1966. https://doi.org/10.1512/iumj.1967.16.16001
H. Fujita and T. Kato. On the Navier-Stokes initial value problem. I. Arch. Rational Mech. Anal., 16:269–315, 1964. https://doi.org/10.1007/BF00276188
S. Gala. On regularity criteria for the three-dimensional micropolar fluid equations in the critical Morrey-Campanato space. Nonlinear Anal. Real World Appl., 12(4):2142–2150, 2011. https://doi.org/10.1016/j.nonrwa.2010.12.028
S. Gala. A remark on the logarithmically improved regularity criterion for the micropolar fluid equations in terms of the pressure. Math. Methods Appl. Sci., 34(16):1945–1953, 2011. https://doi.org/10.1002/mma.1488
G.P. Galdi and S. Rionero. A note on the existence and uniqueness of solutions of the micropolar fluid equations. Internat. J. Engrg. Sci., 15(2):105–108, 1977. https://doi.org/10.1016/0020-7225(77)90025-8
C. He. Regularity for solutions to the Navier-Stokes equations with one velocity component regular. Electron. J. Differential Equations, pp. No. 29, 13, 2002.
L. Iskauriaza, G.A. Ser¨egin and V. Shverak. L3,∞-solutions of Navier-Stokes equations and backward uniqueness. Uspekhi Mat. Nauk, 58(2(350)):3–44, 2003. https://doi.org/10.1070/RM2003v058n02ABEH000609
I. Kukavica and M. Ziane. One component regularity for the Navier-Stokes equations. Nonlinearity, 19(2):453–469, 2006. https://doi.org/10.1088/0951-7715/19/2/012
P.G. Lemari´e-Rieusset. The Navier-Stokes equations in the critical Morrey-Campanato space. Rev. Mat. Iberoam., 23(3):897–930, 2007. https://doi.org/10.4171/RMI/518
S. Machihara and T. Ozawa. Interpolation inequalities in Besov spaces. Proc. Amer. Math. Soc., 131(5):1553–1556, 2003. https://doi.org/10.1090/S0002-9939-02-06715-1
J. Neustupa, A. Novotný and P. Penel. An interior regularity of a weak solution to the Navier-Stokes equations in dependence on one component of velocity. In Topics in mathematical fluid mechanics, volume 10 of Quad. Mat., pp. 163–183. Dept. Math., Seconda Univ. Napoli, Caserta, 2002.
J. Neustupa and P. Penel. Regularity of a suitable weak solution to the NavierStokes equations as a consequence of regularity of one velocity component. In Applied nonlinear analysis, pp. 391–402. Kluwer/Plenum, New York, 1999. https://doi.org/10.1007/0-306-47096-9_26
T. Ohyama. Interior regularity of weak solutions of the timedependent Navier-Stokes equation. Proc. Japan Acad., 36:273–277, 1960. https://doi.org/10.3792/pja/1195524029
E. Ortega-Torres and M. Rojas-Medar. On the regularity for solutions of the micropolar fluid equations. Rend. Semin. Mat. Univ. Padova, 122:27–37, 2009. https://doi.org/10.4171/RSMUP/122-3
P. Penel and M. Pokorný. Some new regularity criteria for the Navier-Stokes equations containing gradient of the velocity. Appl. Math., 49(5):483–493, 2004. https://doi.org/10.1023/B:APOM.0000048124.64244.7e
G. Prodi. Un teorema di unicità per le equazioni di Navier-Stokes. Ann. Mat. Pura Appl., 48:173–182, 1959. https://doi.org/10.1007/BF02410664
J. Serrin. On the interior regularity of weak solutions of the Navier-Stokes equations. Arch. Rational Mech. Anal., 9:187–195, 1962. https://doi.org/10.1007/BF00253344
J. Serrin. The initial value problem for the Navier-Stokes equations. In Nonlinear Problems (Proc. Sympos., Madison, Wis., 1962), pp. 69–98. Univ. Wisconsin Press, Madison, Wis., 1963.
S. Takahashi. On interior regularity criteria for weak solutions of the Navier-Stokes equations. Manuscripta Math., 69(3):237–254, 1990. https://doi.org/10.1007/BF02567922
G. Łukaszewicz. Micropolar fluids. Modeling and Simulation in Science, Engineering and Technology. Theory and applications. Birkhäuser Boston, Inc., Boston, MA, 1999. https://doi.org/10.1007/978-1-4612-0641-5
B. Yuan. On regularity criteria for weak solutions to the micropolar fluid equations in Lorentz space. Proc. Amer. Math. Soc., 138(6):2025–2036, 2010. https://doi.org/10.1090/S0002-9939-10-10232-9
Y. Zhou. A new regularity criterion for the Navier-Stokes equations in terms of the gradient of one velocity component. Methods Appl. Anal., 9(4):563–578, 2002. https://doi.org/10.4310/MAA.2002.v9.n4.a5
Y. Zhou. A new regularity criterion for weak solutions to the NavierStokes equations. J. Math. Pures Appl. (9), 84(11):1496–1514, 2005. https://doi.org/10.1016/j.matpur.2005.07.003
Y. Zhou and M. Pokorný. On the regularity of the solutions of the NavierStokes equations via one velocity component. Nonlinearity, 23(5):1097–1107, 2010. https://doi.org/10.1088/0951-7715/23/5/004
